我的世界Forge mod开发-绘制线段以及曲线
起因
我在学习制作forgemod 的ui,需要画一条线段于是去查了官方文档https://docs.neoforged.net/docs/gui/screens#gui-graphics发现官方的 GuiGraphics 只能绘制水平线和垂直线
我接着翻看mc源码,发现想要绘制线段需要通过官方封装的com.mojang.blaze3d接口直接调用opengl绘制图形
那好吧我就自己封装一个LineBuilder来画连续线段吧
具体绘制过程
绘制逻辑
首先要通过screen传入的guigraphics获得即将要渲染的顶点矩阵
并创建bufferbuilder来修改顶点矩阵
private final Matrix4f pose;
private final BufferBuilder bufferbuilder = Tesselator.getInstance().getBuilder(); //创建bufferbuilder
public LineBuilder(@NonNull GuiGraphics graphics) {
pose = graphics.pose().last().pose();
bufferbuilder.begin(VertexFormat.Mode.TRIANGLE_STRIP, DefaultVertexFormat.POSITION_COLOR);
}这里可以看到顶点绘制模式是TRIANGLE_STRIP 三角形而不是 LINE_STRIP 线,这是因为OpenGL的线会有很多局限性,比如设置线的粗细很麻烦
那三角形如何绘制线段呢
很简单,只需要这样

向线段两个顶点的两个垂直方向延申所需宽度的1/2就可以得到四个顶点来绘制TRIANGLE_STRIP
为什么不用QUADS 应为TRIANGLE_STRIP 更灵活,why?
接下来处理折线情况
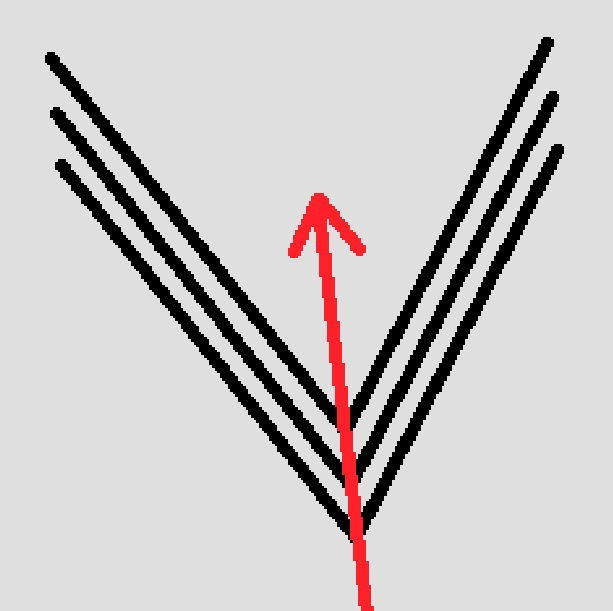
折点部分的顶点需要沿着折点的平分线方向延申宽度的1/2就可以得出
还需要处理面朝向问题
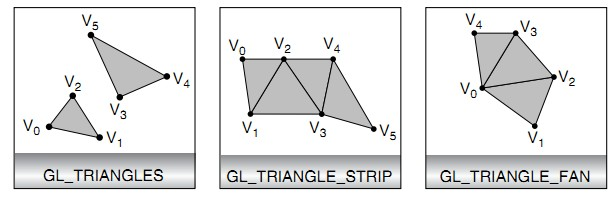
GL_TRIANGLES是以每三个顶点绘制一个三角形。第一个三角形使用顶点v0,v1,v2,第二个使用v3,v4,v5,以此类推。如果顶点的个数n不是3的倍数,那么最后的1个或者2个顶点会被忽略。
GL_TRIANGLE_STRIP则稍微有点复杂。
其规律是:
构建当前三角形的顶点的连接顺序依赖于要和前面已经出现过的2个顶点组成三角形的当前顶点的序号的奇偶性(如果从0开始):
如果当前顶点是奇数:
组成三角形的顶点排列顺序:T = [n-1 n-2 n].
如果当前顶点是偶数:
组成三角形的顶点排列顺序:T = [n-2 n-21 n].
以上图为例,第一个三角形,顶点v2序号是2,是偶数,则顶点排列顺序是v0,v1,v2。第二个三角形,顶点v3序号是3,是奇数,则顶点排列顺序是v2,v1,v3,第三个三角形,顶点v4序号是4,是偶数,则顶点排列顺序是v2,v3,v4,以此类推。
如果顺序有误会导致面被剔除直接不显示等渲染问题,比如这样
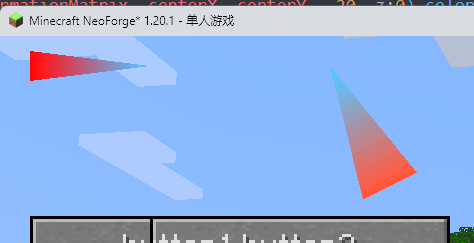
好多三角面消失了
可以使用RenderSystem.disableCull(); 直接禁用背面剔除,但是这样还是会有渲染问题
完整LineBuilder
package fun.sakuraspark.sakuracore.graphics;
import org.checkerframework.checker.nullness.qual.NonNull;
import org.joml.Matrix4f;
import org.joml.Vector2f;
import com.mojang.blaze3d.vertex.BufferBuilder;
import com.mojang.blaze3d.vertex.BufferBuilder.RenderedBuffer;
import com.mojang.blaze3d.vertex.DefaultVertexFormat;
import com.mojang.blaze3d.vertex.Tesselator;
import com.mojang.blaze3d.vertex.VertexFormat;
import net.minecraft.client.gui.GuiGraphics;
/**
* 线条构建器,用于在Minecraft的GUI中绘制平滑、有厚度的线条。
* 使用三角形带(triangle strip)渲染模式来创建线条,支持颜色和线宽的动态调整。
* 处理了线条连接处的平滑过渡,避免了锐角处的视觉问题。
*/
public class LineBuilder {
private final Matrix4f pose;
private final BufferBuilder bufferbuilder = Tesselator.getInstance().getBuilder();;
private Vector2f last_vertex;
private int last_color = 0xFFFFFFFF;
private float last_weight = 1.0f;
private Vector2f this_vertex;
private int this_color = 0xFFFFFFFF;
private float this_weight = 1.0f;
private Vector2f next_vertex;
private int next_color = 0xFFFFFFFF;
private float next_weight = 1.0f;
/**
* 创建一个新的线条构建器
*
* @param graphics GUI图形上下文,用于获取变换矩阵
*/
public LineBuilder(@NonNull GuiGraphics graphics) {
pose = graphics.pose().last().pose();
bufferbuilder.begin(VertexFormat.Mode.TRIANGLE_STRIP, DefaultVertexFormat.POSITION_COLOR);
}
/**
* 设置下一个顶点的坐标
*
* @param x 顶点的X坐标
* @param y 顶点的Y坐标
* @return 返回线条构建器实例,支持链式调用
*/
public LineBuilder vertex(float x, float y) {
next_vertex = new Vector2f(x, y);
return this;
}
/**
* 设置下一个顶点的颜色
*
* @param color ARGB格式的颜色值
* @return 返回线条构建器实例,支持链式调用
*/
public LineBuilder color(int color) {
next_color = color;
return this;
}
/**
* 设置下一段线条的粗细
*
* @param weight 线条粗细,默认为1.0f
* @return 返回线条构建器实例,支持链式调用
*/
public LineBuilder weight(float weight) {
next_weight = weight;
return this;
}
/**
* 完成当前顶点的添加,并计算线段的渲染信息
* <p>
* 处理线段的连接处,确保线条在拐角处平滑过渡。对于锐角,会自动调整以避免过度膨胀。
* 此方法需要在设置完顶点、颜色和粗细后调用。
*
* @return 返回线条构建器实例,支持链式调用
*/
public LineBuilder endVertex() {
if (this_vertex == null) {
this_vertex = next_vertex;
this_color = next_color;
this_weight = next_weight;
return this;
}
if (last_vertex == null) {
last_vertex = this_vertex;
last_color = this_color;
last_weight = this_weight;
this_vertex = next_vertex;
this_color = next_color;
this_weight = next_weight;
Vector2f vector2f = new Vector2f(-(this_vertex.y - last_vertex.y), (this_vertex.x - last_vertex.x)).normalize();
float dx = vector2f.x / 2.0f * last_weight;
float dy = vector2f.y / 2.0f * last_weight;
bufferbuilder.vertex(pose, last_vertex.x - dx, last_vertex.y - dy, 0).color(last_color).endVertex();
bufferbuilder.vertex(pose, last_vertex.x + dx, last_vertex.y + dy, 0).color(last_color).endVertex();
return this;
}
// 计算当前点的法向量(两条线段的角平分线)
Vector2f prevSegment = new Vector2f(last_vertex.x - this_vertex.x, last_vertex.y - this_vertex.y).normalize();
Vector2f nextSegment = new Vector2f(next_vertex.x - this_vertex.x, next_vertex.y - this_vertex.y).normalize();
// 计算前一段的法线向量,用于确定角平分线的方向和共线情况下的偏移方向
Vector2f prevNormal = new Vector2f(-(this_vertex.y - last_vertex.y), (this_vertex.x - last_vertex.x));
if (prevNormal.lengthSquared() < 1e-12f) { // 处理 last_vertex 和 this_vertex 重合的罕见情况
// 如果 prevNormal 长度为0,尝试使用 nextSegment 的法线
// 这是一个边缘情况,理想情况下输入点不应导致这种情况
// 如果 nextSegment 也无效,则无法计算法线,可能需要默认值或抛出错误
// 这里简单地基于 nextSegment 计算一个法线 (如果 nextSegment 有效)
if (nextSegment.lengthSquared() > 1e-12f) {
prevNormal.set(-nextSegment.y, nextSegment.x).normalize(); // 使用 nextSegment 的法线
} else {
// 如果两个段都无效(例如,所有三个点都重合),则无法形成线段
// 可以选择返回或使用一个默认的 bisector,例如 (0,1)
// 但这通常表示输入数据有问题
// 为了简单起见,如果 prevNormal 无法计算,后续逻辑可能会出问题
// 但原始代码在此情况下 prevSegment.normalize() 也会产生 NaN
// 此处我们先确保 prevNormal 被 normalize,即使它是 (0,0) normalize 后的 NaN
prevNormal.normalize(); // 会产生 NaN 如果长度为0
}
} else {
prevNormal.normalize();
}
Vector2f bisector = new Vector2f(); // 初始化 bisector
Vector2f sumPrevNext = new Vector2f(prevSegment).add(nextSegment);
// 检查 prevSegment 和 nextSegment 是否几乎方向相反(表明三点共线且 this_vertex 在中间)
// 当它们的和接近零向量时,表明角度接近180度。
// 使用 lengthSquared() 比 length() 更高效,因为它避免了平方根运算。
// 1e-8f 是一个较小的阈值 (例如 1e-4f * 1e-4f)
if (sumPrevNext.lengthSquared() < 1e-8f) {
// 三点共线,形成直线。此时 "角平分线" 未良好定义或计算不稳定。
// 直接使用前一段的法向量 prevNormal 作为偏移方向。
// prevNormal 已经是归一化的。
bisector.set(prevNormal);
// 在这种情况下,prevNormal.dot(bisector) 将是 prevNormal.dot(prevNormal) = 1 (因为它们相同且已归一化),
// 这不小于0,所以不会翻转 bisector,这对于直线是正确的。
} else {
// 正常情况:存在一个角度,计算角平分线向量。
bisector.set(sumPrevNext).normalize();
// 确保 bisector 的方向与 prevNormal 定义的“外侧”一致,
// 以保证三角形带顶点的一致缠绕顺序。
if (prevNormal.dot(bisector) < 0) {
// 如果方向不一致,翻转bisector
bisector.mul(-1);
}
}
// 确保生成的向量是垂直于路径方向的 // 注释:bisector 此处是斜接法线方向
// 计算缩放因子 - 处理锐角情况
float sinHalfAngle = (float) Math.sqrt((1.0f - prevSegment.dot(nextSegment)) / 2.0f);
float scale = sinHalfAngle > 0.0001f ? 1.0f / sinHalfAngle : 1.0f;
scale = Math.min(scale, 2.0f); // 限制最大缩放以避免尖角处过度膨胀
float dx = bisector.x / 2.0f * this_weight * scale;
float dy = bisector.y / 2.0f * this_weight * scale;
// 保持顶点添加的一致顺序
bufferbuilder.vertex(pose, this_vertex.x - dx, this_vertex.y - dy, 0).color(this_color).endVertex();
bufferbuilder.vertex(pose, this_vertex.x + dx, this_vertex.y + dy, 0).color(this_color).endVertex();
last_vertex = this_vertex;
last_color = this_color;
last_weight = this_weight;
this_vertex = next_vertex;
this_color = next_color;
this_weight = next_weight;
return this;
}
/**
* 完成线条的构建,返回渲染缓冲区
* <p>
* 添加最后一个顶点并结束三角形带的构建。此方法应在所有顶点都添加完成后调用。
*
* @return 包含线条渲染数据的缓冲区
*/
public RenderedBuffer end() {
Vector2f vector2f = new Vector2f(-(this_vertex.y - last_vertex.y), (this_vertex.x - last_vertex.x)).normalize();
float dx = vector2f.x / 2.0f * this_weight;
float dy = vector2f.y / 2.0f * this_weight;
bufferbuilder.vertex(pose, this_vertex.x - dx, this_vertex.y - dy, 0).color(this_color).endVertex();
bufferbuilder.vertex(pose, this_vertex.x + dx, this_vertex.y + dy, 0).color(this_color).endVertex();
return bufferbuilder.end();
}
}
使用示例
RenderSystem.setShader(GameRenderer::getPositionColorShader);
RenderSystem.disableDepthTest();
//RenderSystem.disableCull(); 背面剔除,不需要了
RenderSystem.enableBlend();
RenderSystem.defaultBlendFunc();
graphics.hLine(centerX-100, centerY-100, centerY-50, 0xFFFF0000);
LineBuilder lineBuilder = new LineBuilder(graphics);
lineBuilder.vertex(10, 10).color(0xFFFF0000).weight(8).endVertex()
.vertex(50, 10).color(0xFF3EC0FF).weight(5).endVertex()
.vertex(70, 50).color(0xFFF74C30).weight(3).endVertex()
.vertex(90, 10).color(0xFF9BE96F).endVertex()
.vertex(110, 10).color(0xFF3EC0FF).endVertex()
.vertex(130, 50).color(0xFFF74C30).endVertex();
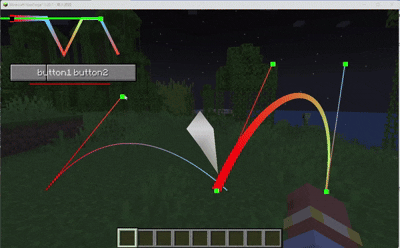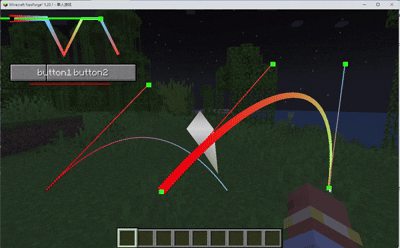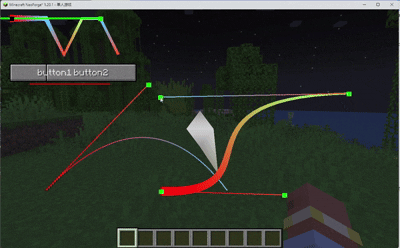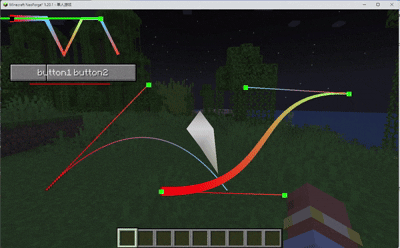
BufferUploader.drawWithShader(lineBuilder.end());效果

恭喜你得到了可以绘制颜色厚度渐变的连续线段
拓展
曲线
那么如何绘制曲线呢?
上过小学的都知道一个正方形一直切就能切成一个圆,那么只要个一小段画个折线,只要分段够多你就能得到

一条平滑的曲线🤣
再加上贝塞尔计算和一点点的代码你就得到